Построение логического выражения по заданной таблице истинности

Что такое логический элемент?

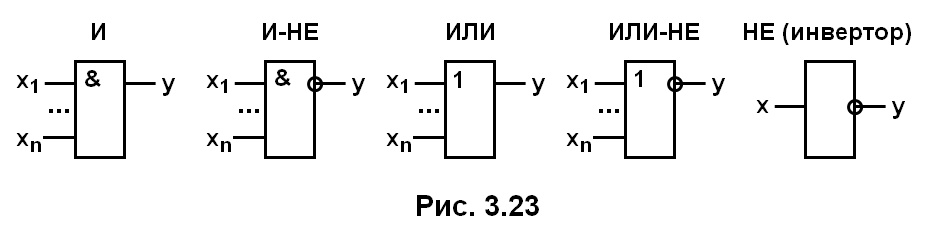
Логический элемент (логический вентиль) — это электронная схема, выполняющая некоторую простейшую логическую операцию. На рис. 3.23 приведены примеры условных графических обозначений некоторых логических элементов.

Логический элемент может быть реализован в виде отдельной интегральной схемы. Часто интегральная схема содержит несколько логических элементов.

Логические элементы используются в устройствах цифровой электроники (логических устройствах) для выполнения простого преобразования логических сигналов.

Рассмотрим наиболее широко используемую исторически сложившуюся классификацию. Она построена и с учетом того, какие электронные приборы являются основными в соответствующих интегральных схемах, и с учетом особенностей использованных схемотехнических решений.

Классы логических элементов

Выделяются следующие классы логических элементов (так называемые логики):

• резисторно-транзисторная логика (РТЛ);
• диодно-транзисторная логика (ДТЛ);
• транзисторно-транзисторная логика (ТТЛ);
• эмиттерно-связанная логика (ЭСЛ);
• транзисторно-транзисторная логика с диодами Шоттки (ТТЛШ);
• логика на основе МОП-транзисторов с каналами типа p(p-МДП);
• логика на основе МОП-транзисторов с каналами типа n(n-МДП);
• логика на основе комплементарных ключей на МДП-транзисторах (КМДП, КМОП);
• интегральная инжекционная логика И2Л;
• логика на основе полупроводника из арсенида галлия GaAs;

В настоящее время наиболее широко используются следующие логики: ТТЛ, ТТЛШ, КМОП, ЭСЛ. Устарела и практически не используется РТЛ. Для разрабатываемых в настоящее время устройств можно рекомендовать использовать КМОП-логику, а также логику на основе GaAs.

Логические элементы и другие цифровые электронные устройства выпускаются в составе серий микросхем. Серия микросхем — это совокупность микросхем, характеризуемых общими технологическими и схемотехнически­ми решениями, а также уровнями электрических сигналов и напряжения питания.

Приведенная классификация охватывает не только собственно логические элементы, но и другие цифровые устройства, в том числе микропроцессорные. Однако здесь следует учитывать, что при производстве сложных цифровых устройств некоторые логики не использовались и не используются.

Промышленные серии логики

Примеры серии микросхем:ТТЛ − К155, КМ155, К133, КМ133;ТТЛШ − 530, КР531, КМ531, КР1531, 533, К555, КМ555, 1533, КР1533;ЭСЛ − 100, К500, К1500;КМОП — 564, К561, 1564, КР1554;GaAs-К6500;

Каждая серия микросхем, несмотря на то, что она обычно содержит самые разнообразные цифровые устройства, характеризуется некоторым набором параметров, дающих достаточно подробное представление об этой серии. При определении этих параметров ориентируются именно на логические элементы — простейшие устройства серии микросхем. В соответствии с этим говорят о параметрах не серии микросхем, а о параметрах логических элементов данной серии.

Параметры логических элементов

Быстродействие характеризуют временем задержки распространения сигнала tзр и максимальной рабочей частотой Fмaкс. Обратимся к идеализированным временным диаграммам, соответствующим элементу НЕ (инвертору) (рис. 3.24).

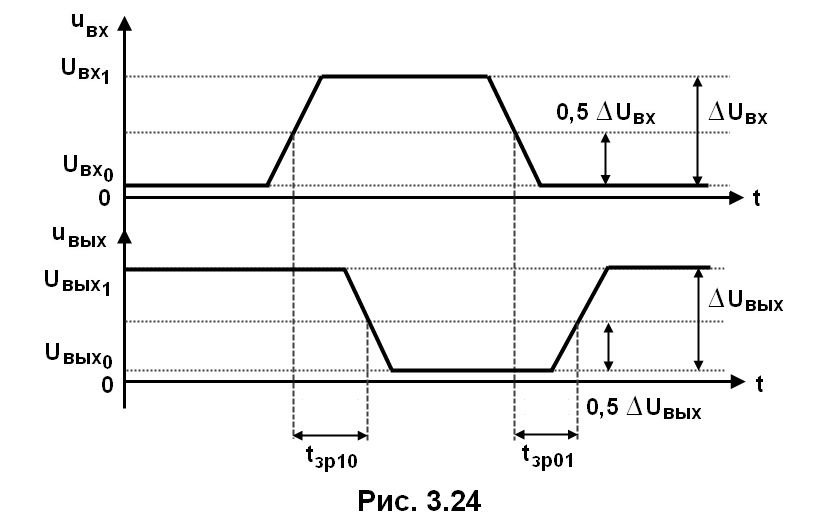
Через Uвхl и Uвыxl обозначены уровни входного и выходного напряжений, соответствующие логической единице, а через Uвх0 и Uвыx0 — соответствующие логическому нулю. Различают время задержки tзр10 распространения при переключении из состояния 1 в состояние 0 и при переключении из состояния 0 в состояние 1 — tзр01, а также среднее время задержки распространения tзр , причем

tзр = 0,5 · ( tзр10 + tзр01)

Васильев Дмитрий Петрович Профессор электротехники СПбГПУ

Время задержки принято определять по перепадам уровней 0,5∆Uвх и 0,5∆Uвыx. Максимальная рабочая частота Fмaкс — это частота, при которой сохраняется работоспособность схемы.

Нагрузочная способность характеризуется коэффициентом объединения по входу K оби коэффициентом разветвления по выходу Kраз (иногда используют термин «коэффициент объединения по выходу»). Величина K об — это число логических входов, величина K раз — максимальное число однотипных логических элементов, которые могут быть подключены к выходу данного логического элемента. Типичные значения их таковы:

Kоб= 2…8, K раз = 4…10. Для элементов с повышенной нагрузочной способностью K раз = 20…30.

Помехоустойчивость в статическом режиме характеризуют напряжением Uпст, которое называют статической помехоустойчивостью. Это такое максимально допустимое напряжение статической помехи на входе, при котором еще не происходит изменение выходных уровней логического элемента.

Важным параметром является мощность, потребляемая микросхемой от источника питания. Если эта мощность различна для двух логических состояний, то часто указывают среднюю потребляемую мощность для этих состояний.

Важными являются также следующие параметры:

• напряжение питания;
• входные пороговые напряжения высокого и низкого уровня Uвх1.порог и Uвх.0порог, соответствующие изменению состояния логического элемента;
• выходные напряжения высокого и низкого уровней Uвых1 и Uвых0.

Используются и другие параметры.

Конъюнкция или логическое умножение (в теории множеств – это пересечение)

Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.

Обозначение: &, $wedge$, $cdot$.

Таблица истинности для конъюнкции

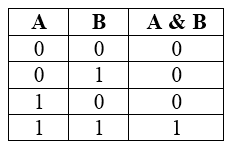
Рисунок 1.

Свойства конъюнкции:

1. Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
2. Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
3. Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).

Готовые работы на аналогичную тему

• 410 руб.Логические операции и их свойстваКурсовая работа
• 260 руб.Логические операции и их свойстваРеферат
• 220 руб.Логические операции и их свойстваКонтрольная работа

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Дизъюнкция или логическое сложение (в теории множеств это объединение)

Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.

Обозначение: +, $vee$.

Таблица истинности для дизъюнкции

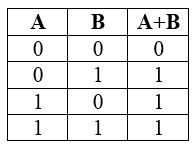
Рисунок 2.

Свойства дизъюнкции:

1. Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
2. Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
3. Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).

Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)

Отрицание — означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.

Обозначения: не $A$, $bar{A}$, $¬A$.

Таблица истинности для инверсии

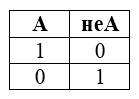
Рисунок 3.

Свойства отрицания:

«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.

Импликация или логическое следование

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).

Обозначения: $to$, $Rightarrow$.

Таблица истинности для импликации

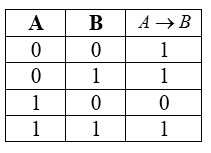
Рисунок 4.

Свойства импликации:

1. $A to B = ¬A vee B$.
2. Импликация $A to B$ ложна, если $A=1$ и $B=0$.
3. Если $A=0$, то импликация $A to B$ истинна при любом значении $B$, (из лжи может следовать истинна).

Эквивалентность или логическая равнозначность

Эквивалентность — это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.

Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.

Таблица истинности для эквивалентности

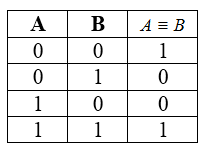
Рисунок 5.

Свойства эквивалентности:

1. Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
2. КНФ $A equiv B = (bar{A} vee B) cdot (A cdot bar{B})$
3. ДНФ $A equiv B = bar{A} cdot bar{B} vee A cdot B$

Задача анализа логических схем

Задача анализа заключается в определении функции f, реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

1. Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
2. Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
3. Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
4. Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

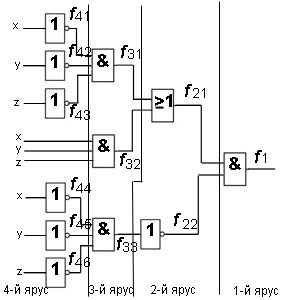
Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение

Пример 2. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Правильное решение и ответ .

Пример 3. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

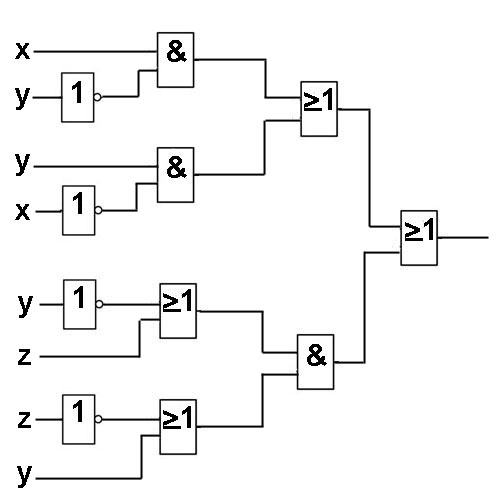
Продолжаем искать булеву функцию логической схемы вместе

Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

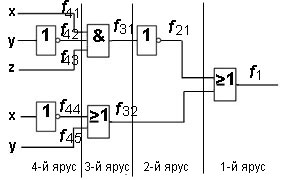
Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

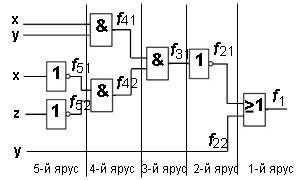
Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Задача синтеза логических схем в булевом базисе

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

x	y	f
1	1	0
1	0	0
0	1	1
0	0	0

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y. В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:

0	0	0
0	1	0
1	1	1
0	1	0

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией получаем следующую логическую схему:

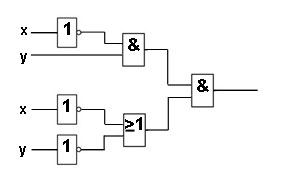
А теперь очередь дошла до функций алгебры логики четырёх переменных. Сначала выполним синтез логической схемы в булевом базисе.

Пример 7. Построить в булевом базисе логическую схему, реализующую функцию алгебры логики

Решение. Для построения логической схемы потребуются 4 схемы «НЕ», одна трёхвходовая схема «И», 2 двухвходовые схемы «И» и одна трёхвходовая схема «ИЛИ». В соответствии с этим получаем следующую логическую схему:

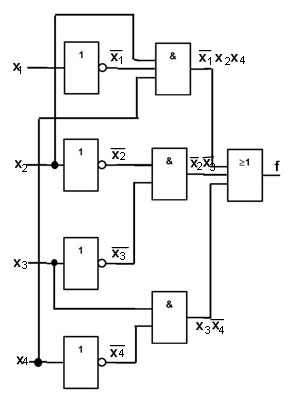
Примеры решения задач «Логические основы работы компьютера»

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

№1.

Дана логическая функция: F(А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.

Решение:

Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:

• первым  выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;
• далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.

Выход инвертора является выходом функциональной схемы.

Изобразим схему, следуя данным действиям:

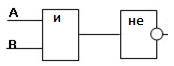
№2.

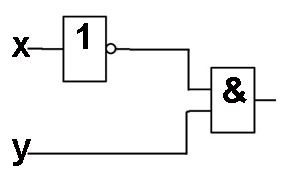
Определите логическую функцию, соответствующую заданной функциональной схеме:

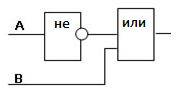
Решение:

Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.

Итак, последовательность действий:

• ¬A — сигнал входа А инвертирован;
• ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.

Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:

F(A, B) = ¬A / B

Ответ: F(A, B) = ¬A / B

№3.

Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.

Решение:

Значение логического выражения  — 1

№4.

Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.

Решение:

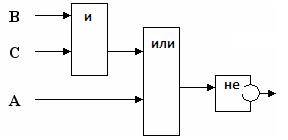
Значение логического выражения  — 1

Примеры

Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:

• Штрих Шеффера.
• Стрелка Пирса.
• Определение эквивалентности.

Штрих Шеффера

Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:

А	Б	А и Б	не (А и Б)
Л	Л	Л	И
Л	И	Л	И
И	Л	Л	И
И	И	И	Л

Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.

Стрелка Пирса

Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:

А	Б	А или Б	не (А или Б)
Л	Л	Л	И
Л	И	И	Л
И	Л	И	И
И	И	И	Л

А	Б	не А	не Б	не А и не Б
Л	Л	И	И	И
Л	И	И	Л	Л
И	Л	Л	И	И
И	И	Л	Л	Л

Значения выражений совпали. Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.

Определение эквивалентности

Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».

Здесь две переменных и пять действий. Строим таблицу:

А	Б	В = (из А следует Б)	Г = (из Б следует А)	Д = А эквивалентно Б	Е = В и Г	Д эквивалентно Е
Л	Л	И	И	И	И	И
Л	И	И	Л	Л	Л	И
И	Л	Л	И	Л	Л	И
И	И	И	И	И	И	И

В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.