Аналоговый ввод

Аналоговое и цифровое представление сигнала

4. Аналоговый ввод

Цифровая обработка сигналов обладает многими преимуществами. В связи с этим перед обработкой в компьютере аналоговые сигналы преобразуются в цифровую форму. Цифровым сигналом называется такой сигнал, который может принимать ограниченный ряд значений зависимых и независимых переменных. Независимыми переменными обычно являются время или координаты, а зависимыми - амплитуда.

Цифровые (дискретные) сигналы окружают нас повсюду. Телефонные компании используют цифровые сигналы для представления человеческого голоса. Радио, телевизионные и высококачественные звуковые системы - все используют поэтапное преобразование сигнала в цифровую форму из-за ее безукоризненной точности воспроизведения, подавления шумов и больших возможностей обработки сигналов. Снимки NASA удаленных планет и космического пространства часто подвергаются цифровой обработке для удаления шумов и выделения полезной информации. Данные в экономической области, результаты переписи населения и цены акций на фондовой бирже - все это доступно в цифровом виде.

Дискретизация сигналов

Для получения аналогового сигнала вы, прежде всего, должны преобразовать его в дискретное представление. На практике под этим понимается использование аналого- цифрового преобразователя (АЦП). Рассмотрим аналоговый сигнал х(t), который дискретизируется каждые t секунд. Временной интервал t называют интервалом дискретизации или периодом дискретизации. Обратная величина, 1/t, известна как частота дискретизации или частота выборки с единицей измерения - количество выборок в секунду. Каждое из дискретных значений x(t) в моменты времени t = 0, t, 2t, 3t и т.д. называются выборками. Таким образом, х(0), x(t), х(2t), ... образуют полный набор выборок. Сигнал х(t) может быть представлен дискретным набором выборок, как это показано в следующем уравнении: {x(0), х(t), x(2t), x(3t), ...,x(kt), ...}

Следующий рисунок демонстрирует аналоговый сигнал и соответствующую ему оцифрованную версию. Выборки заданы в дискретные моменты времени.

Частота выборки

Один из наиболее важных параметров измерительной системы с аналоговым вводом или выводом является частота, с которой измерительное устройство производит выборку входного сигнала или генерацию выходного. Частота сканирования или частота выборки в АЦП определяет, насколько часто имеет место аналого-цифровое или цифро-аналоговое преобразование. При большей частоте выборки собирается больше точек за данное время, что позволяет построить лучшее представление исходного сигнала, чем при низкой частоте выборки. Генерация одногерцового сигнала с использованием 1000 точек на период при частоте 1000 выборок в секунду создает гораздо более точное представление, чем использование 10 точек на период при частоте 10 Выб/сек.

Наложение частот

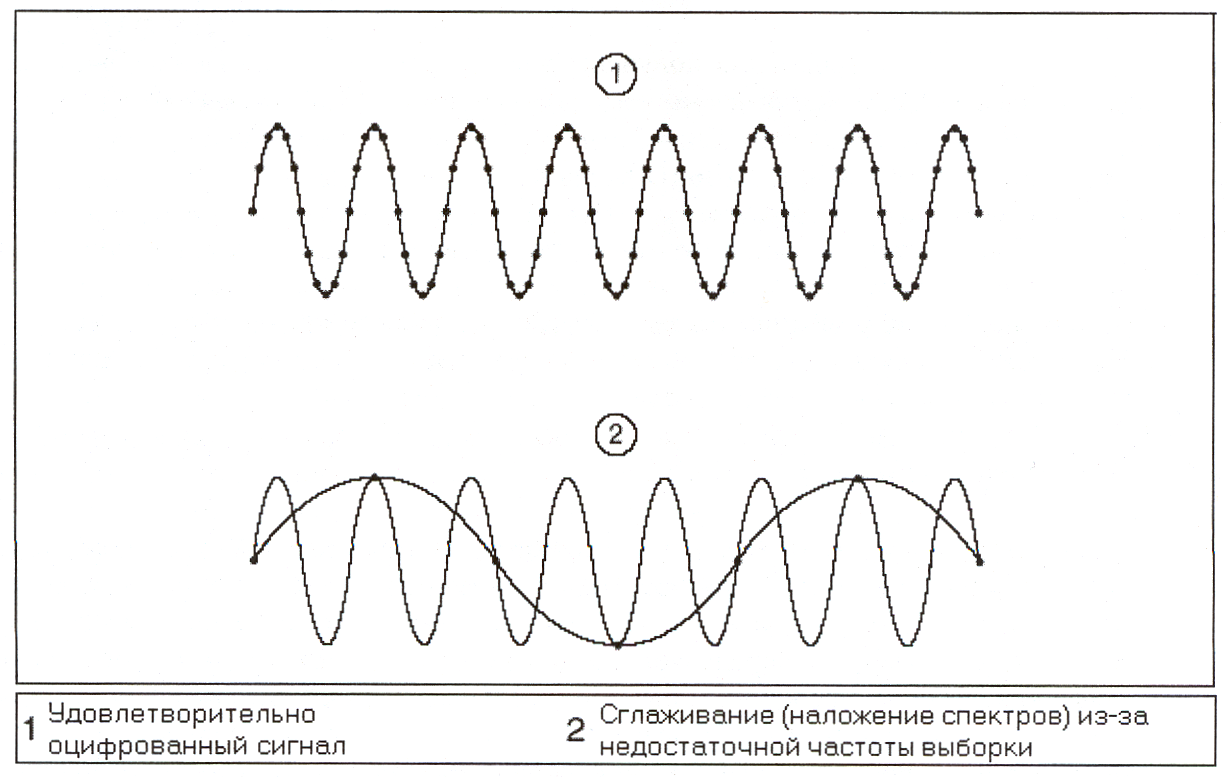
Слишком низкая частота выборки приводит к такому явлению, как наложение частот (aliasing), что вызывает искажение в представлении аналогового сигнала. Недостаточная скорость оцифровки является причиной того, что сигнал выглядит так, как будто его частота отлична от действительной. Чтобы избежать наложения частот оцифровку производят с частотой, большей частоты самого сигнала. Следующая иллюстрация показывает удовлетворительно оцифрованный сигнал и эффект наложения частот из-за недостаточной частоты выборки.

Для точного представления частоты сигнала при измерениях вы должны производить выборки с частотой, большей удвоенной максимальной частотной компоненты сигнала, в соответствии с теоремой Найквиста. Частота Найквиста - это максимальная частота сигнала, при которой его можно точно представить без эффекта наложения частот с данной частотой выборки. Частота Найквиста равна половине частоты выборки. В сигналах, имеющих частотные компоненты, превышающие частоту Найквиста, появятся ложные низкочастотные составляющие. Частота этой составляющей равна по модулю разности между частотой входного сигнала и наиболее близкой частотой, равной целому числу, умноженному на частоту выборки. 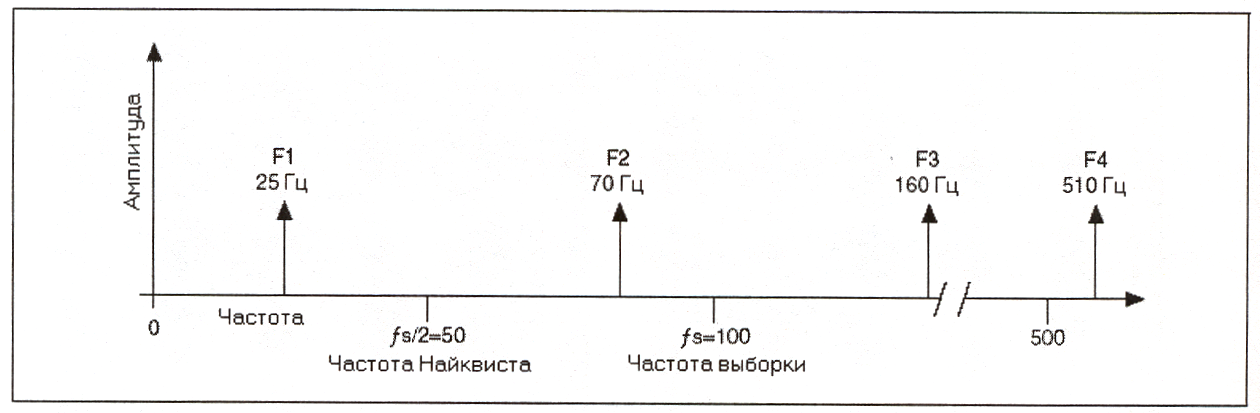Например, положим, что частота выборки f_s равна 100 Гц. Предположим также, что входной сигнал содержит компоненты с частотами: 25 Гц, 70 Гц, 160 Гц и 510 Гц, как показано на следующем рисунке.

Частотные компоненты ниже частоты Найквиста (f_s/2 = 50 Гц) оцифровываются правильно. Это показано на следующей иллюстрации. Частотные компоненты выше частоты Найквиста появляются как побочные. Например, F₁ (25 Гц) появляется на правильной частоте, a F₂ (70 Гц), F₃ (160 Гц) и F₄ (510 Гц) имеют низкочастотные ложные компоненты на частотах 30 Гц, 40 Гц и 10 Гц, соответственно.

Для вычисления ложных частот используйте следующее выражение: Ложная частота = Абсолютное значение (Наиболее близкая частота, равная целому числу, умноженному на частоту выборки - Частота входного сигнала). Например, ложная F₂ = |100 - 70| = 30 Гц; ложная F₃ = |(2) 100 - 160| = 40 Гц; ложная F₄ = |(5)100 - 510| = 10 Гц.

Определение частоты выборки

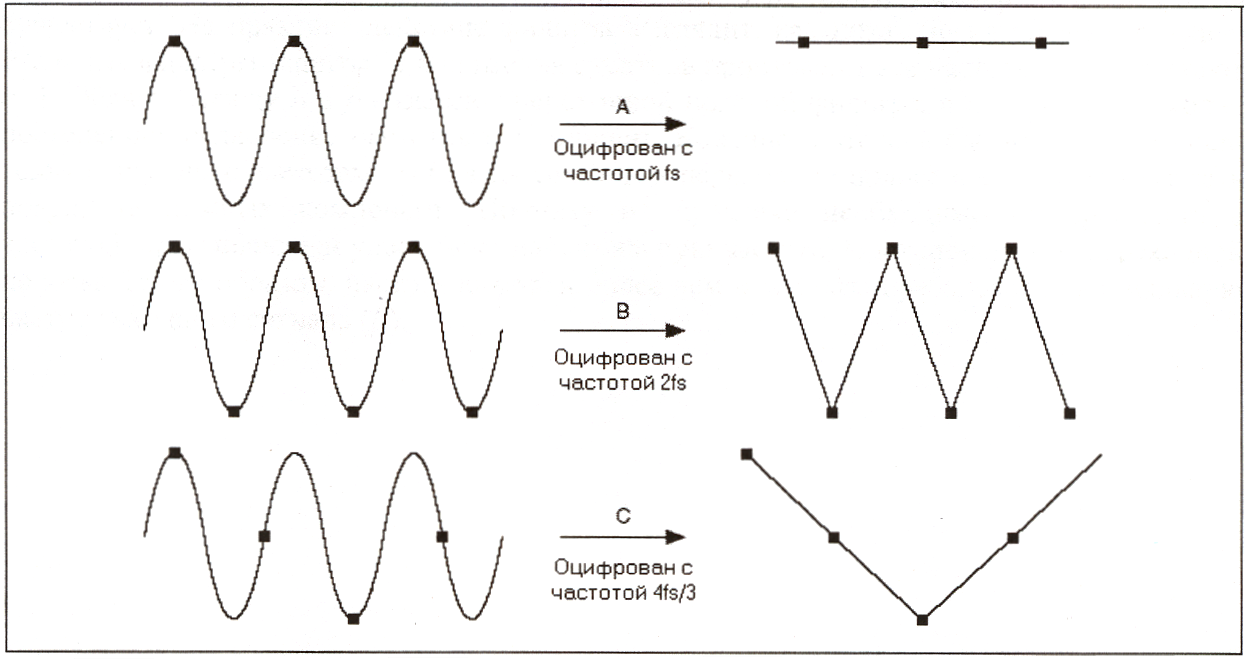
Возможно, вы захотите осуществлять выборку с максимально возможной частотой для данного измерительного устройства. Однако если вы оцифровываете очень быстро в течение длительных промежутков времени, то вам может не хватить оперативной памяти или дискового пространства для накопления данных. Следующая иллюстрация показывает влияние различных частот оцифровки на принимаемый сигнал.

Пример А: оцифровка синусоидального сигнала частотой f и с такой же частотой дискретизации f_s. В результате, полученные выборки образуют постоянный сигнал. Однако если вы увеличите частоту оцифровки до 2f_s, то оцифрованная осциллограмма будет иметь ту же частоту (или то же количество циклов), что и исходная осциллограмма, но будет выглядеть как треугольный сигнал, что показано на Примере В. Значительно увеличивая частоту дискретизации по сравнению с fs, вы можете более точно воспроизвести осциллограмму. В Примере С частота выборки равна 4f_s/3. Поскольку в этом случае частота Найквиста меньше f_s, (4f_s/3 х 1)/2 = 2f_s/3), то будет воспроизводиться осциллограмма с неправильной частотой и формой.

Теорема Найквиста является отправной точкой при выборе достаточной частоты выборки - она должна в два раза превышать максимальную частотную компоненту в сигнале. К сожалению, этой частоты обычно не хватает для практических целей. Сигналы, встречающиеся в реальных приложениях, часто содержат составляющие, лежащие выше частоты Найквиста. Это приводит к добавлению ложных компонент в точно оцифрованный сигнал, что создает искаженные цифровые данные. Поэтому, на практике, выборку производят с частотой, многократно превышающей частоту входного сигнала. Для промышленных приложений является обычным превышение в 5-10 раз.