|
|
Счётчики. Асинхронные счётчики
Введение в цифровую схемотехнику
10. Счётчики. Асинхронные счётчики
Счетчики представляют собой более высокий, чем регистры, уровень сложности цифровых микросхем, имеющих внутреннюю память. Хотя в основе любого счетчика лежат те же самые триггеры, которые образуют и регистры, но в счетчиках триггеры соединены более сложными связями, в результате чего их функции - сложнее, и на их основе можно строить более сложные устройства, чем на регистрах. Точно так же, как и в случае регистров, внутренняя память счетчиков - оперативная, то есть ее содержимое сохраняется только до тех пор, пока включено питание схемы. С выключением питания память стирается, а при новом включении питания схемы содержимое памяти будет произвольным, случайным, зависящим только от конкретной микросхемы, то есть выходные сигналы счетчиков будут произвольными.
|
|
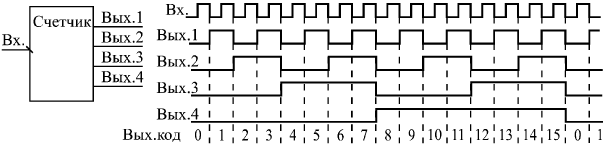
Работа 4-разрядного двоичного счетчика
|
Асинхронные счетчики
Асинхронные счетчики строятся из простой цепочки JK-триггеров, каждый из которых работает в счетном режиме. Выходной сигнал каждого триггера служит входным сигналом для следующего триггера. Поэтому все разряды (выходы) асинхронного счетчика переключаются последовательно (отсюда название - последовательные счетчики), один за другим, начиная с младшего и кончая старшим. Каждый следующий разряд переключается с задержкой относительно предыдущего, то есть, вообще говоря, асинхронно, не одновременно с входным сигналом и с другими разрядами.
|
|
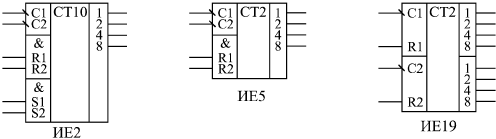
Асинхронные счетчики стандартных серий
|
Чем больше разрядов имеет счетчик, тем большее время ему требуется на полное переключение всех разрядов. Задержка переключения каждого разряда примерно равна задержке триггера, а полная задержка установления кода на выходе счетчика равна задержке одного разряда, умноженной на число разрядов счетчика. Легко заметить, что при периоде входного сигнала, меньшем полной задержки установления кода счетчика, правильный код на выходе счетчика просто не успеет установиться, поэтому такая ситуация не имеет смысла. Это накладывает жесткие ограничения на период (частоту) входного сигнала, причем увеличение, к примеру, вдвое количества разрядов счетчика автоматически уменьшает вдвое предельно допустимую частоту входного сигнала.
|
|
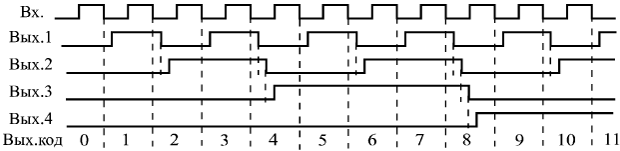
Временная диаграмма работы 4-разрядного асинхронного счетчика
|
Основное применение асинхронных счетчиков состоит в построении всевозможных делителей частоты, то есть устройств, выдающих выходной сигнал с частотой, в несколько раз меньшей, чем частота входного сигнала. В данном случае нас интересует не выходной код счетчика, то есть не все его разряды одновременно, а только один разряд, поэтому взаимные задержки отдельных разрядов не играют роли, полная задержка переключения счетчика не имеет значения. Простейший пример делителя частоты на два - это триггер в счетном режиме или счетчик, выходным сигналом которого является выход первого, младшего разряда 1.
При построении делителей частоты иногда важна не только частота выходного сигнала, но и его форма, его скважность, то есть отношение периода следования импульсов к длительности этих импульсов. В таких случаях чаще всего требуется меандр - цифровой сигнал со скважностью, равной двум (длительность импульсов равна длительности паузы между ними). Получить меандр из любого сигнала довольно просто: надо использовать дополнительный делитель частоты на 2, правда, при этом частота выходного сигнала уменьшится еще вдвое.
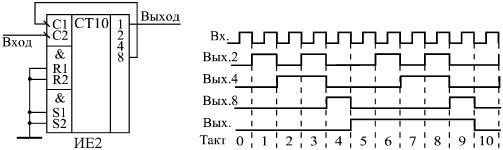
В делителе использован счетчик ИЕ2, у которого одноразрядный внутренний счетчик включен после трехразрядного внутреннего счетчика. Трехразрядный счетчик делит частоту входного сигнала на 5, но выходные импульсы имеют скважность, не равную двум (она равна 5). Одноразрядный счетчик делит частоту еще вдвое и одновременно формирует меандр. Задержки переключения разрядов счетчика относительно друг друга на рисунке не показаны (применяем первый уровень представления, логическую модель).
|
|
Делитель частоты на 10, выдающий меандр
|
Иногда возникает задача деления частоты входного сигнала в произвольное число раз (не в 10 и не в 2n, что легко обеспечивается самой структурой стандартных счетчиков). В этом случае можно организовать сброс счетчика при достижении им требуемого кода путем введения обратных связей.
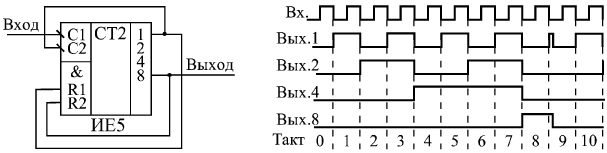
Например, на рис. показан простейший делитель частоты на 9 на основе счетчика ИЕ5. При достижении его выходным кодом значения 9 (то есть 1001) счетчик автоматически сбрасывается в нуль по входам R1 и R2, и счет начинается снова. В результате частота выходного сигнала в 9 раз меньше частоты входного сигнала. При этом скважность выходного сигнала не равна двум. Временная диаграмма показана на рисунке для первого уровня представления (без учета временных задержек).
|
|
Делитель частоты на 9 с обратными связями
|
Если в числе, на которое надо делить частоту, больше двух единиц (например, 15, то есть 1111, или 13, то есть 1101), то для формирования сигнала сброса надо использовать элементы 2И, 3И или 4И, чтобы объединить все выходы, равные единице. В результате можно построить делитель входной частоты в любое число раз от 2 до 2N, где N - число разрядов используемого счетчика. Правда, при организации обратных связей надо учитывать ограничение на быстродействие счетчика. Все разряды, используемые для обратной связи, должны успеть переключиться за один период входного сигнала. Скважность выходного сигнала может принимать в данном случае самые разные значения, например, выходной сигнал может представлять собой очень короткие импульсы.
Оригинальный источник материала:
Новиков Ю.В. Основы цифровой схемотехники: базовые элементы и схемы, методы проектирования. — М.: Мир, 2001, 379 с.
Сайт автора(ов):
www.yury-novikov.narod.ru
|
|
|

